OS CTF

Crypto/Cipher Conundrum

Solution

In this challenge, multiple steps are required to decrypt the encrypted text.

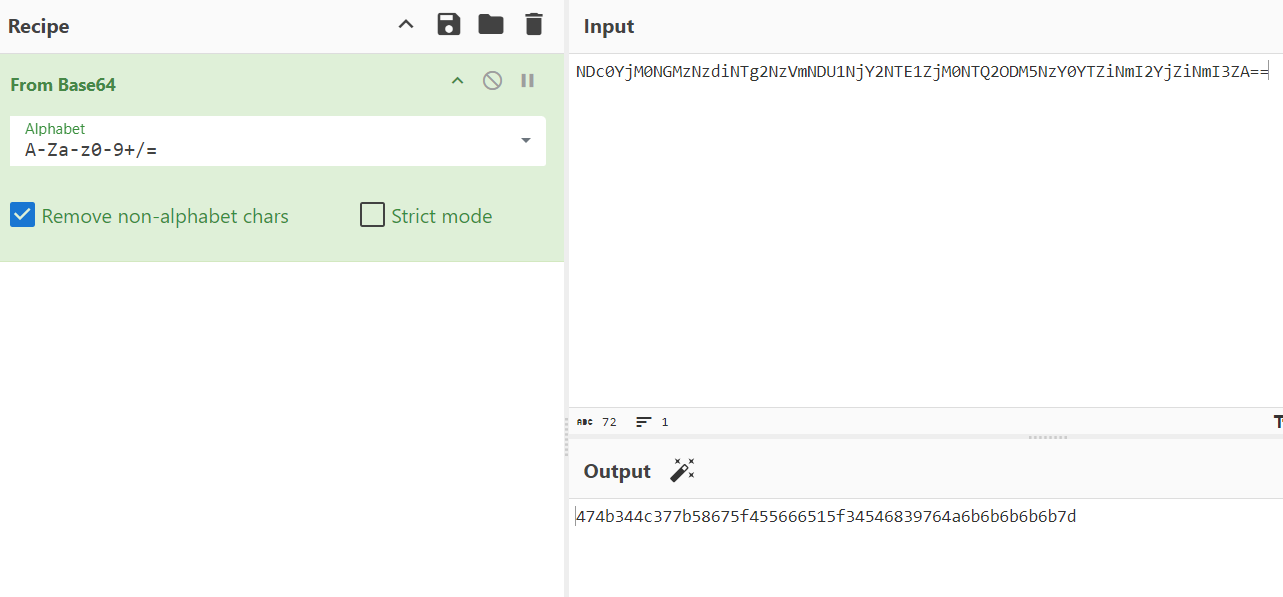
• Base64:

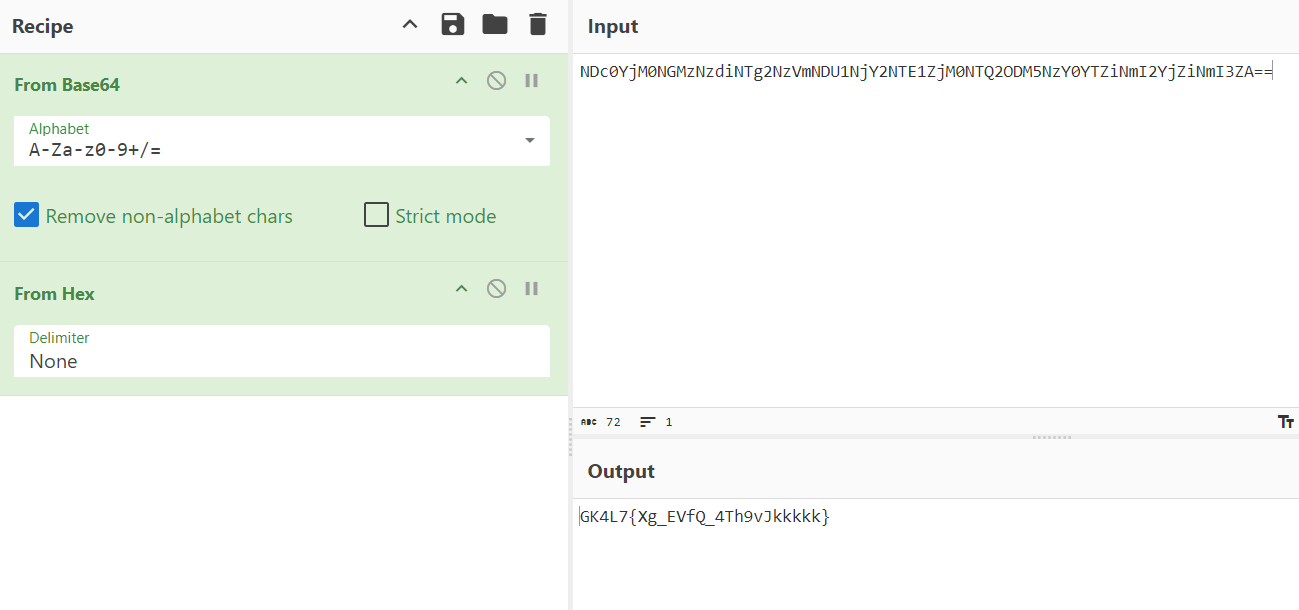
• Hex:

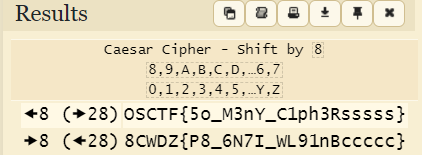
• Caesar cipher:

We successfully decrypted it to reveal the flag.

Flag:

OSCTF{5o_M3nY_C1ph3Rsssss}

Crypto/Couple Primes

Challenge Description:

We are given a RSA encryption setup and the parameters n and c.

from Crypto.Util.number import *
from sympy import nextprime

flag = b'REDACTED'

p = getPrime(1024)
q = nextprime(p)
e = 65537

n = p * q
c = pow(bytes_to_long(flag), e, n)

print(f"n = {n}")
print(f"c = {c}")

Solution:

To decrypt the ciphertext c to retrieve the flag, we need to factorize n to find the primes p and q. Given that q is the next prime after p, we can use this property to find the primes.

Here is the complete solution:

from Crypto.Util.number import long_to_bytes
from sympy import nextprime, isprime
from math import isqrt

n = 2015988416886389917712817571503042966646173328566017066425504857911626508776326874833382086091327167458698083908809269723033
6179818435879126554509868570255414201418619851045615744211750178240471758695923469393333600480843090831767416937814471973060610730578620506577745372347777922355677932755542699210313287595362584505135967456855068550375989801913361017083952090117041405458626488736811460716474071561590513778196334141517893224697977911862004615690183334216587398645213023148750443295007000911541566340284156527080509545145423451091853688188705902833261507474200445477515893168405730493924172626222872760780966427
c = 18440162368010249375653348677429595229051180035668845001125855048750591059785630865891877031796050869136099359028540172514890273415892550857190509410541828375948243175466417949548148007390803680005616875833010137407850955608659023797782656930905693262770473679394796595557898347900786445803645539553815614140428316398058138450937721961593146082399553119578102712100359284788650328835784603011091312735813903241087475279011862693938914825685547337081335030237385061397899718079346063519325222861490101383929790275635381333028091769118083102339908694751574572782030287570280071809896532329742115422479473386147281509394
e = 65537

approx_p = isqrt(n)

while not isprime(approx_p):
    approx_p -= 1

p = approx_p
q = nextprime(p)

assert p * q == n

phi = (p - 1) * (q - 1)
d = pow(e, -1, phi)

m = pow(c, d, n)
flag = long_to_bytes(m)

print(flag.decode())

Flag:

OSCTF{m4y_7h3_pR1m3_10v3_34cH_07h3r?}