Dice CTF

Crytography/winter

Challenge Description:

Provided Files

• server.py

Solution:

The provided code (server.py) implements a signature scheme using a modified version of the Winternitz One-Time Signature (WOTS) scheme. It includes methods for key generation, signing, and verification.

1. Key Generation: The keygen method will generate a secret key (sk) and a corresponding verification key (vk).
2. Signing: The sign method takes a message a message (msg) as input and produces a signature (sig) using the secrrect key (sk).
3. Verification: The verrify method wil verify whether a given signature (sig) corresponds to a given message (msg) using the verification key (vk).

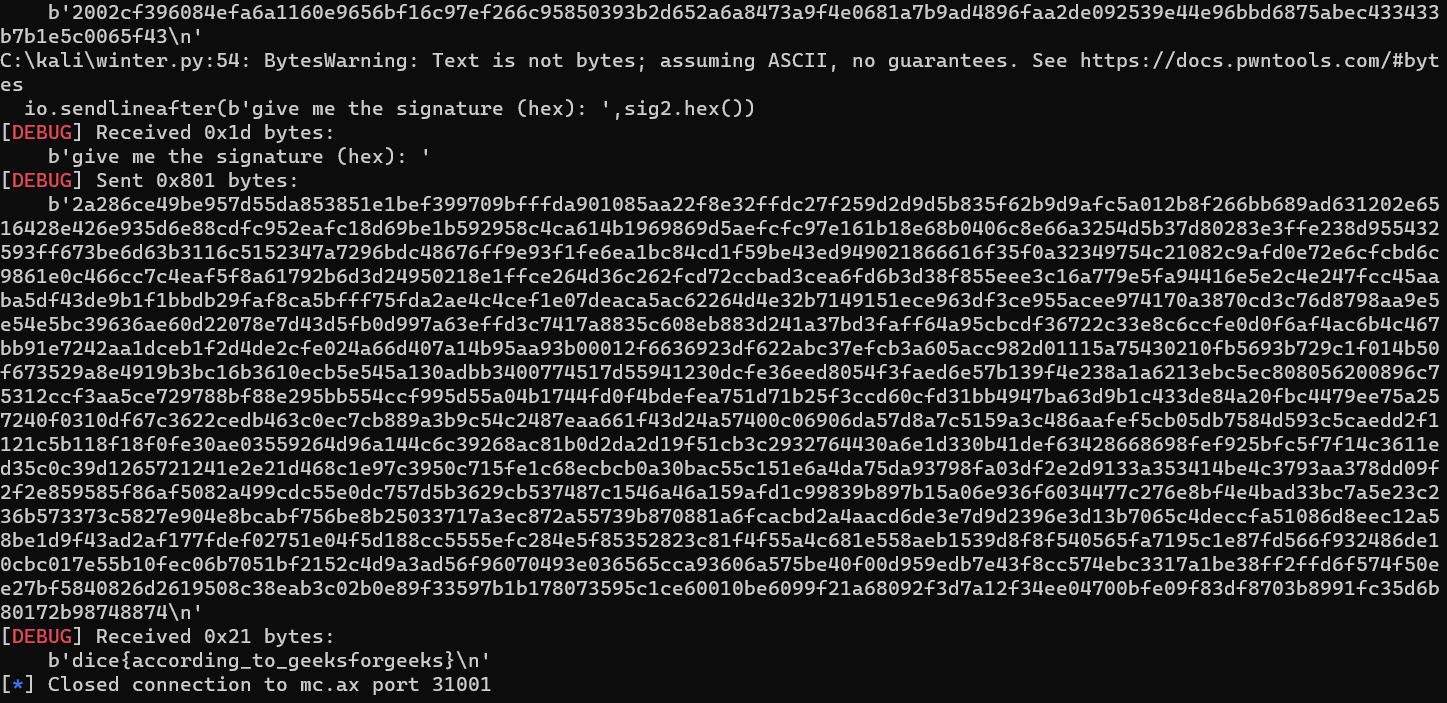
Initially, the challenge will prompt to enter another message in hexadecimal format. After sending the message, the server responds with the corresponding signature. After that, another message in hexadecimal format and a valid signature for this second message were required. Thus, the first signature is crucial for verifying the message’s authenticity during the second stage.

from hashlib import sha256
import os

# Find two msg that meet the conditions
if 1:
    tmax = 255
    tmin = 0
    msgmin = os.urandom(64)
    msgmax = os.urandom(64)
    s2 = sha256(msgmin).digest()
    s1 = sha256(msgmax).digest()
    while True:
        msg1 = os.urandom(64)
        ss = sha256(msg1).digest()
        if max(list(ss)) < tmax:
            tmax = max(list(ss))
            msgmin = msg1
            s2 = sha256(msgmin).digest()
            print("max", tmax, list(s1), msg1)
        if min(list(ss)) > tmin:
            tmin = min(list(ss))
            msgmax = msg1
            s1 = sha256(msgmax).digest()
            print("min", tmin, list(s1), msg1)
        if s1 != s2 and all(i >= j for i, j in zip(s1, s2)):
            break
print(msgmax)
print(msgmin)
print("-----------------------------------------------------------------------------------")

# Find msg1 and msg2
msg1 = msgmax
msg2 = msgmin
s1 = sha256(msg1).digest()
s2 = sha256(msg2).digest()
from pwn import *

context.log_level = "debug"
io = remote("mc.ax", 31001)
io.sendlineafter(b"give me a message (hex): ", msg1.hex().encode())
signature = io.recvline().strip().decode().split(": ")[1]
signature = bytes.fromhex(signature)
print(signature)
chunks = [signature[i : i + 32] for i in range(0, len(signature), 32)]
print(len(chunks), chunks)


def hash(x, n):
    for _ in range(n):
        x = sha256(x).digest()
    return x


sig2 = b""
for i, c in enumerate(chunks):
    sig2 += hash(c, s1[i] - s2[i])
print(sig2)

io.sendlineafter(b"give me a new message (hex): ", msg2.hex().encode())
io.sendlineafter(b"give me the signature (hex): ", sig2.hex())
io.recvline()

The code will enter a loop that continues until a suitable message pair is found.

Inside the loop:

1. It generates a new random message (msg1).
2. It calculates the SHA-256 hash of the new message (ss).
3. It checks the maximum (tmax) and minimum (tmin) values encountered so far by comparing them with the individual bytes in the new message hash (ss).
4. If a new maximum byte is found, it updates tmax, msgmin, and s2 (hash of msgmin).
5. Similarly, if a new minimum byte is found, it updates tmin, msgmax, and s1 (hash of msgmax).

The loop continues until it finds two messages (msgmax and msgmin) where the hash of msgmax (s1) has all bits greater than or equal to the corresponding bits in the hash of msgmin (s2).

In the second part of the code, after generating two messages (msg1 and msg2) that meet specific conditions, the script connects to the server and sends the first message (msg1). It receives the corresponding signature from the server and then modifies this signature based on the difference between the hash values of msg1 and msg2. Lastly, it sends msg2 along with sig2.

Flag:

dice{according_to_geeksforgeeks}

Web/dicedicegoose

Challenge Description:

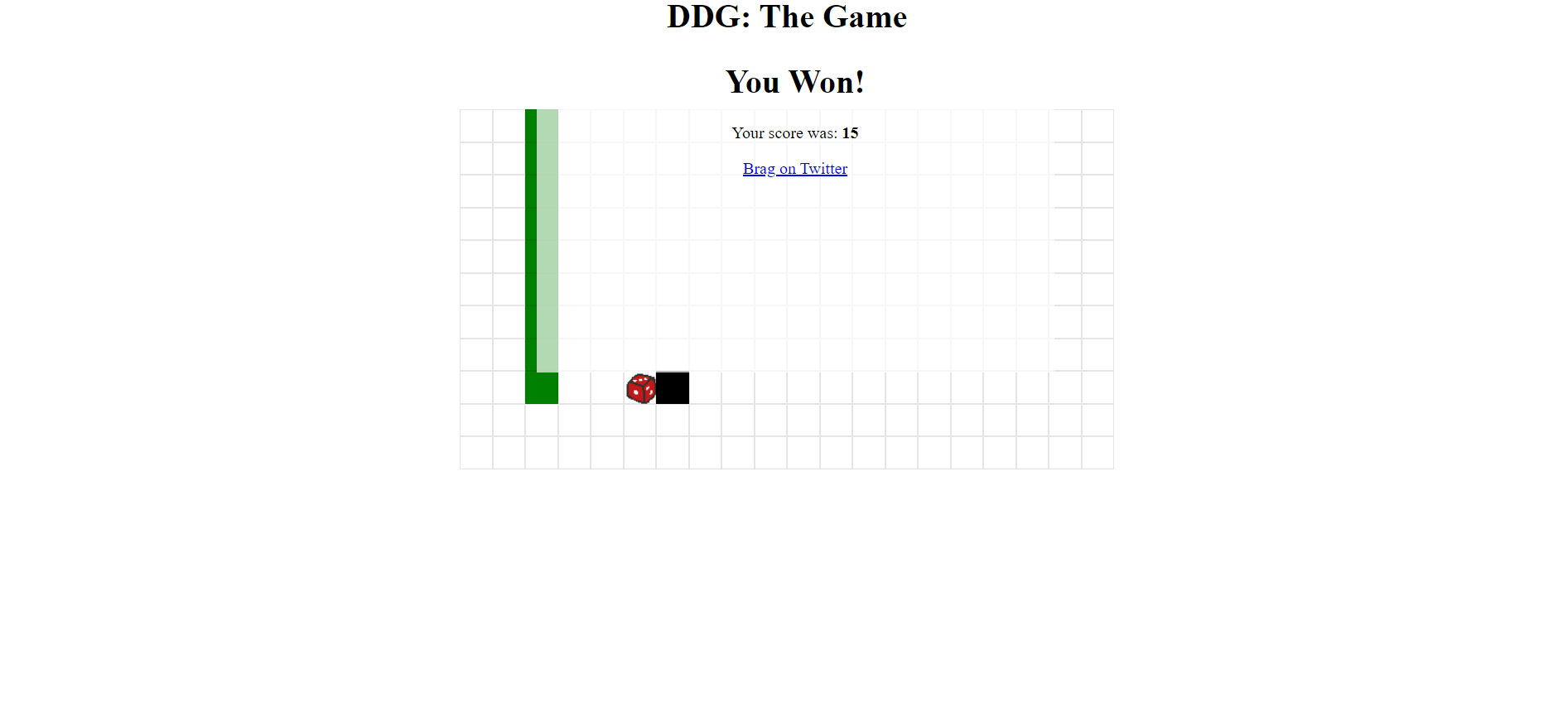
It is a grid-based game where the player controls a dice that must navigate through a grid to touch a black box (goose) to win the game. The grid contains obstacles (walls) that the player must avoid.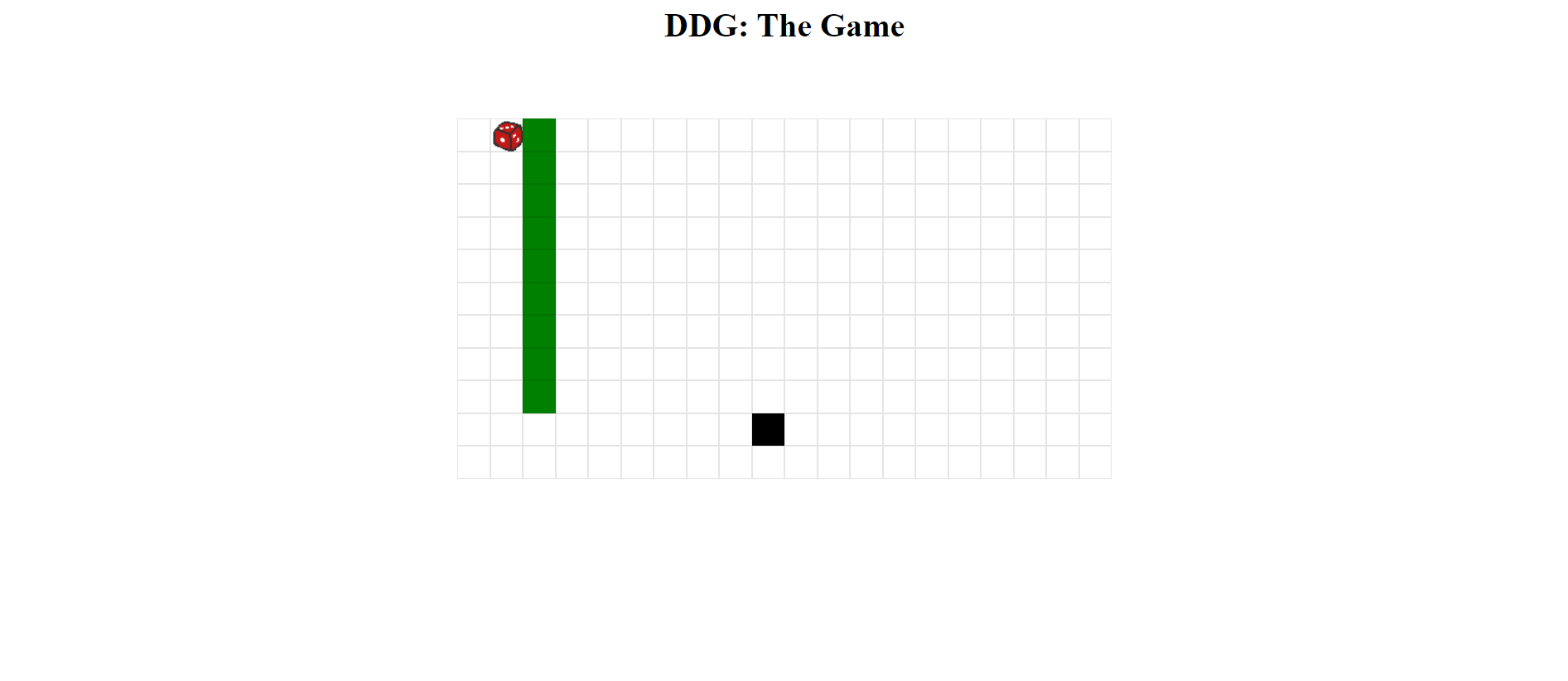

The player wins by reaching the same position as the goose (black box).

Solution:

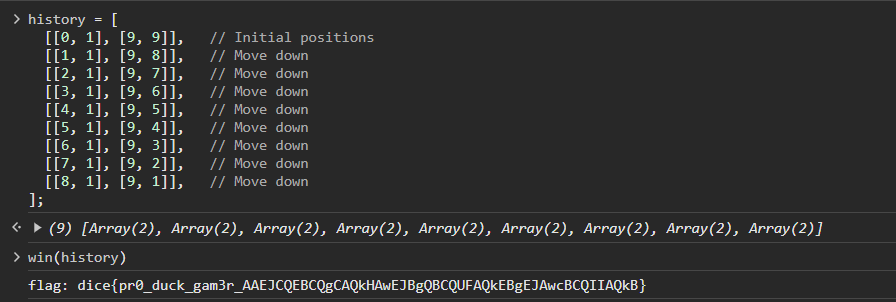
I found an interesting function while analyzing the code. If the player’s score is exactly 9 moves, the function logs a special flag associated with a hidden code. This function, named win(history), is triggered when the player wins the game by reaching the goose. The crucial part of the function checks if the player’s score is exactly 9 moves, and if so, it will log a special flag. This indicates that winning the game in exactly 9 moves is a unique condition that reveals the flag.

  function win(history) {
    const code = encode(history) + ";" + prompt("Name?");

    const saveURL = location.origin + "?code=" + code;
    displaywrapper.classList.remove("hidden");

    const score = history.length;

    display.children[1].innerHTML = "Your score was: <b>" + score + "</b>";
    display.children[2].href =
      "https://twitter.com/intent/tweet?text=" +
      encodeURIComponent(
        "Can you beat my score of " + score + " in Dice Dice Goose?",
      ) +
      "&url=" +
      encodeURIComponent(saveURL);

    if (score === 9) log("flag: dice{pr0_duck_gam3r_" + encode(history) + "}");
  }

I also found that the history is built in a specific array format. The history array tracks the positions of the player and the goose at each move.

  let player = [0, 1];
  let goose = [9, 9];

  let walls = [];
  for (let i = 0; i < 9; i++) {
    walls.push([i, 2]);
  }

  let history = [];
  history.push([player, goose]);

To trigger the flag condition, we need to build the history array such that the game is won in exactly 9 moves. Here’s an example of how the history array might look for 9 moves:

history = [
  [[0, 1], [9, 9]],  
  [[1, 1], [9, 8]],  
  [[2, 1], [9, 7]],  
  [[3, 1], [9, 6]],  
  [[4, 1], [9, 5]],  
  [[5, 1], [9, 4]],  
  [[6, 1], [9, 3]],  
  [[7, 1], [9, 2]],  
  [[8, 1], [9, 1]], 
];

Finally, we need to execute this array and to call the win(history) function with the built history array.

Flag:

dice{pr0_duck_gam3r_AAEJCQEBCQgCAQkHAwEJBgQBCQUFAQkEBgEJAwcBCQIIAQkB}